Problems 1-4 Mass Points

Problem Posts

Problem 1-4 (Geometry) [Difficulty 1]

QUESTION
(Classic) $D$ bisects side $AB$ of triangle $ABC$. $E$ is on $AC$ so that $AE:EC=1:2$. $CD$ and $BE$ meet at $G$. Find $DG:GC$.

Overview

Mass Points.

Discussion

This problem is a hackneyed staple, and so much has been said about using areas and side lengths. Perhaps mass points are not yet so popular a method:

Give me a place to stand, and I will move the earth. 

So Archimedes boasts, but it's probable that the lever he'd use would have to be more rigid than any known material. But in the wonder world of mathematics, line segments don't bend nor break.

Mass point geometry assigns a mass $m$ to each point $P$; it's convenient to note this mass point as $mP$. The nice idea is that given two mass points $mA$ and $nB$, you can "summon" balancing point $\left(m+n\right)M$ on segment $AB$ so that $m\cdot AM = n \cdot MB$. 

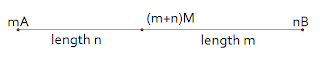Most of the time we assign masses to deliberately make a given point a balancing point.

What does this have to do with the cevian problem (by the way, a cevian is this, and the word is pronounced such)? With the given distance ratios, we can assign masses with the expectation that the foot of each cevian is be a balancing point of the endpoints of its corresponding side. Then, make the concurrency point the balancing point for each cevian.

Now we're in business! So long as you have one center of mass (one concurrency point), you can go about filling out the other masses and deducing the side ratios. (The answer is $1:4$.) Feels like magic compared to using area formulas, doesn't it?

Much, much more has been said about this powerful technique (split masses for multiple systems), and I'll let these excellent resources here and here speak for themselves.