 |
 |
Problem Posts |  |
 |
 |
 |
Part 3 of 4 of How Many Shapes? |  |
 |
While it would be far more fun for me if I jumped from topic to topic, I believe I owe it to you, dear readers, to flog this horse until it's brain dead. Completeness is a virtue.
So last time we finished off the case where we count rectangles in rectangles, even when some 'matchsticks' or grid wires are missing. Now onwards to rectangles in non-rectangles.
CAN WE DO BETTER?
What if the original grid were a rectangle, instead of a square?Or an irregular figure?What if we were counting rectangles instead of squares?What if some of the grid 'wires' are missing?- What if we're working on a triangular grid, counting triangles? Does our logic still apply?
2 Rectangles in Non-Rectangles
This is ad hoc land. The base technique would again be to count one-by-one, but as we will see there are tricks for certain special irregular figures.
2.1 Intersecting Rectangles
QUESTION
As usual, we want a way that's easily generalized. How many rectangles of all sizes in the figure below?
As usual, we want a way that's easily generalized. How many rectangles of all sizes in the figure below?

So I don't confuse myself, let $X$ be the lower $6\times 4$ rectangular grid, and $Y$ be the upper one.
In the given example, it's probably more expedient to count one by one, than to expend time in developing some clever technique. (My personal rule of thumb is to develop a formula for anything with dimension at least 5, but then that's to compensate for my clumsy counting.)
First, let's leverage a simple set theoretic result:
NOTE
Given two finite sets $A$ and $B$,\[\left|A\cup B\right|=\left|A\right|+\left|B\right|-\left|A\cap B\right|\]
Given two finite sets $A$ and $B$,\[\left|A\cup B\right|=\left|A\right|+\left|B\right|-\left|A\cap B\right|\]
Let's first focus on the rectangles that are completely in $X$ and $Y$. That is, they do not straddle both large grids. To count them, we recall that there are \[\binom{7}{2}\binom{5}{2}=210\] rectangles within $X$, and the same for $Y$.
Here's one instance of Venning: $210\times 2 = 420$. This double counts the rectangles in the $2\times 3$ intersection of $X$ and $Y$, so we have to subtract them out: $210\times 2 - \binom{4}{2}\binom{3}{2} = 402$.
Now for the messy part: the rectangles that are neither completely in $X$ nor in $Y$ - let's call them straddlers. Note that any such rectangle must be completely contained in one of the two bands (the red or the blue) below.
Let's start with the blue band. When we count rectangles the usual way, we have carte blanche over where a rectangle must begin and end, horizontally and vertically. Not so for a straddler.
While we have the usual $\binom{3}{2} = 3$ choices for $(y_1,y_2)$, there are restrictions for $(x_1,x_2)$. In particular, the straddler must begin horizontally strictly within $X$ and end in $Y$. In short, $0\le x_1 \le 2$ and $7 \le x_2 \le 9$. So, we have $3\cdot \binom{3}{1}^2 = 27$ straddlers on the blue band.
Similarly, we have $\binom{4}{2}\cdot\binom{2}{1}^2 = 24$ straddlers on the red band.
Now do we have to Venn the straddlers? No, since clearly no straddler is in both bands. So we have 61 straddlers all in all, for a total of $\boxed{463}$ rectangles.
2.2 Semi-regular Figures
A common way to test a student's ability to discover a formula behind a counting technique, and apply it properly is to give her some huge semi-regular task so that manual counting is immediately out of the question.
At any rate, one goal I had in mind for Project Phi is to discourage problem memorization, so just as well.
Let's consider the small cases. What if the staircase has $n$ steps:
It looks like a classic case for induction! If you knew how many rectangles there were for an $n$-staircase, shouldn't it be that much easier to count the ones for an $n+1$-staircase?
So suppose we have our $n$-staircase, and add a row of $n+1$ squares at the bottom. How many new rectangles would be formed? They'd all have to be based at the bottom. So we categorize according to their tops:
There are $\binom{n+2}{2}$ height 1 rectangles at the bottom.
There are $\binom{n+1}{2}$ height 2 rectangles at the bottom. (Why?)
There are $\binom{n}{2}$ height 3 rectangles at the bottom.
There are $\binom{n-i+3}{2}$ height $i$ rectangles at the bottom.
And so on, until we have $\binom{2}{2}=1$ height $n+1$ rectangle at the bottom.
So there are \begin{eqnarray*}
\sum_{i=1}^{n+1}\binom{n-i+3}{2} & = & \sum_{i=2}^{n+2}\binom{i}{2}\\
& = & \frac{1}{2}\sum_{i=1}^{n+1}\left(i\right)\left(i-1\right)\\
& = & \frac{1}{2}\sum_{i=1}^{n+1}i^{2}-\frac{1}{2}\sum_{i=1}^{n+1}i\\
& = & \frac{\left(n+1\right)\left(n+2\right)\left(2n+5\right)}{12}-\frac{\left(n+1\right)\left(n+2\right)}{4}\\
& = & \frac{\left(n+1\right)\left(n+2\right)\left(n+3\right)}{6}
\end{eqnarray*} new rectangles.
So all in all we'd have this many rectangles:
\begin{eqnarray*}
\sum_{i=0}^{n-1}\frac{\left(i+1\right)\left(i+2\right)\left(i+3\right)}{6} & = & \frac{1}{6}\sum_{i=0}^{n-1}\left(i^{3}+6i^{2}+11i+6\right)\\
& = & \frac{1}{6}\left(\frac{n^{2}\left(n-1\right)^{2}}{4}\right)+\frac{\left(n-1\right)\left(n\right)\left(2n-1\right)}{6}+\frac{11}{6}\frac{n\left(n-1\right)}{2}\\
& & +n\\
& = & \boxed{\dfrac{1}{24}n\left(n+1\right)\left(n+2\right)\left(n+3\right)}
\end{eqnarray*}
But this gives me an idea for a very powerful and not so ad-hoc technique.
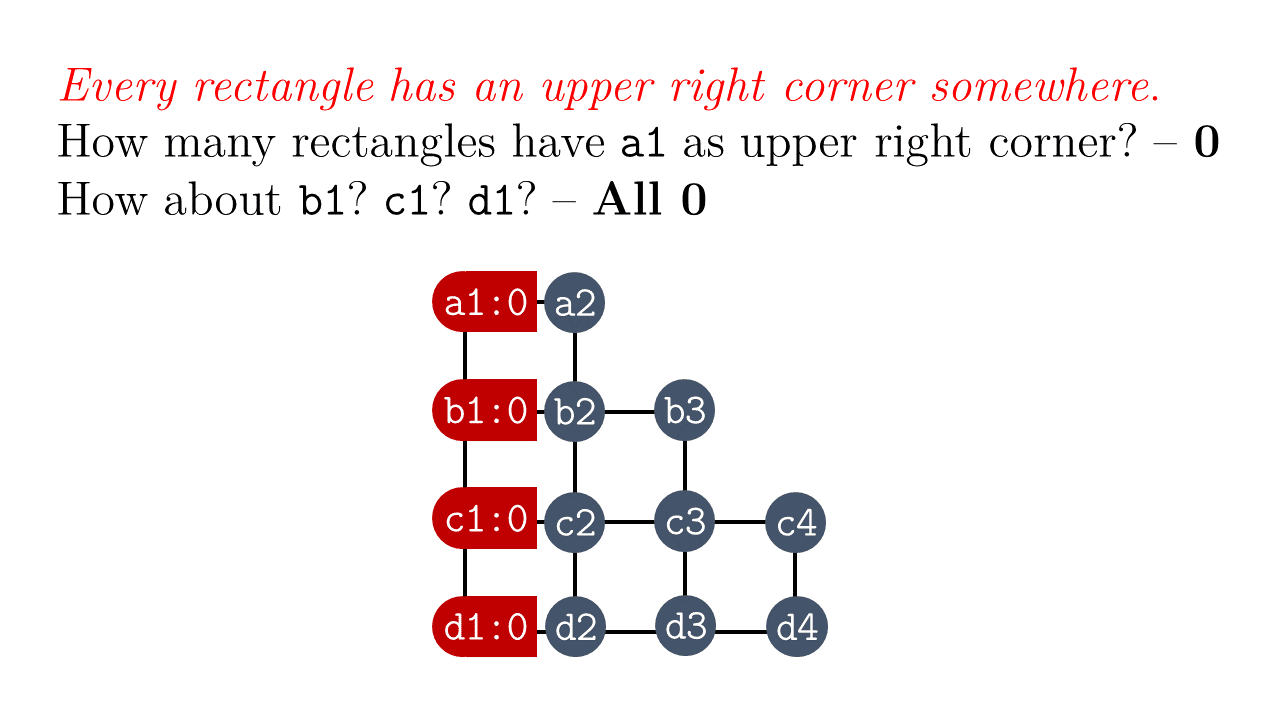
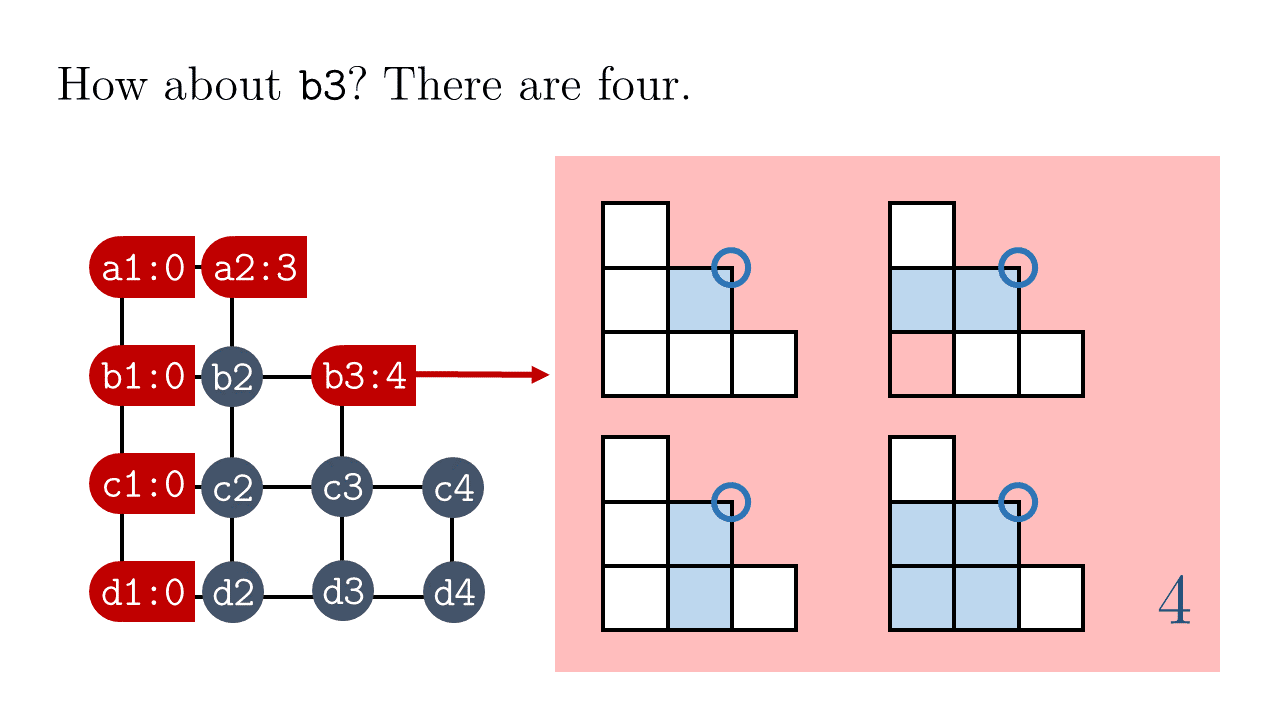
Let's refine what it means to choose a rectangle by $(x_1,x_2,y_1,y_2)$. Essentially this is analogous to picking the coordinates of the upper right corner, then the coordinates of the lower left corner.
We can do just that to our staircase. For every point that can be an upper right corner, we count the number of lower left corners it can be paired with. Below is some clarification:
In the case of the staircase, it's just the multiplication table! In particular, here's the pattern for $n=8$:
\begin{eqnarray}
\sum_{i=1}^{n}\left(n+1-i\right)\sum_{j=1}^{i}j & = & \sum_{i=1}^{n}\frac{i\left(i+1\right)\left(n+1-i\right)}{2}\\
& = & \frac{1}{4}\sum_{i=1}^{n}i\left(i+1\right)\left(n+1-i\right)+\\
& & \left(n+1-i\right)\left(n+2-i\right)i\\
& = & \frac{n+3}{4}\sum_{i=1}^{n}i\left(n+1-i\right)\\
& = & \frac{n+3}{4}\left(\frac{n\left(n+1\right)^{2}}{2}-\frac{n\left(n+1\right)\left(2n+1\right)}{6}\right)\\
& = & \frac{1}{4}n\left(n+1\right)\left(n+3\right)\left(\frac{n+1}{2}-\frac{2n+1}{6}\right)\\
& = & \boxed{\frac{1}{24}n\left(n+1\right)\left(n+2\right)\left(n+3\right)}
\end{eqnarray} which gives us the same answer.
The second step in this computation (equation 2 above) may be a bit confusing. What I did was pair the $i$th term with the $(n+1-i)$th. In the case $n=8$, the first few steps will look like this:
\begin{eqnarray*}
\sum_{i=1}^{8}\left(9-i\right)\sum_{j=1}^{i}j & = & \sum_{i=1}^{8}\frac{i\left(i+1\right)\left(9-i\right)}{2}\\
& = & \frac{1\cdot2\cdot8}{2}+\frac{2\cdot3\cdot7}{2}+\frac{3\cdot4\cdot6}{2}+\frac{4\cdot5\cdot5}{2}\\
& & \frac{5\cdot6\cdot4}{2}+\frac{6\cdot7\cdot3}{2}+\frac{7\cdot8\cdot2}{2}+\frac{8\cdot9\cdot1}{2}\\
& = & \frac{1\cdot\left(2+9\right)\cdot8}{4}+\frac{2\cdot\left(3+8\right)\cdot7}{4}+\frac{3\cdot\left(4+7\right)\cdot6}{4}+\\
& & \frac{4\cdot\left(5+6\right)\cdot5}{4}+\cdots+\frac{8\cdot\left(9+2\right)\cdot1}{4}\\
& = & \frac{11}{4}\left(1\cdot8+2\cdot6+\cdots+8\cdot1\right)\\
& = & \frac{8+3}{4}\sum_{i=1}^{8}i\left(8+1-i\right)
\end{eqnarray*}
At any rate, one goal I had in mind for Project Phi is to discourage problem memorization, so just as well.
QUESTION
How many rectangles?
How many rectangles?
You can try using some PIE argument, or clever semi-manual methods, but I am too lazy for either.
Let's consider the small cases. What if the staircase has $n$ steps:
It looks like a classic case for induction! If you knew how many rectangles there were for an $n$-staircase, shouldn't it be that much easier to count the ones for an $n+1$-staircase?
So suppose we have our $n$-staircase, and add a row of $n+1$ squares at the bottom. How many new rectangles would be formed? They'd all have to be based at the bottom. So we categorize according to their tops:
There are $\binom{n+2}{2}$ height 1 rectangles at the bottom.
There are $\binom{n+1}{2}$ height 2 rectangles at the bottom. (Why?)
There are $\binom{n}{2}$ height 3 rectangles at the bottom.
There are $\binom{n-i+3}{2}$ height $i$ rectangles at the bottom.
And so on, until we have $\binom{2}{2}=1$ height $n+1$ rectangle at the bottom.
So there are \begin{eqnarray*}
\sum_{i=1}^{n+1}\binom{n-i+3}{2} & = & \sum_{i=2}^{n+2}\binom{i}{2}\\
& = & \frac{1}{2}\sum_{i=1}^{n+1}\left(i\right)\left(i-1\right)\\
& = & \frac{1}{2}\sum_{i=1}^{n+1}i^{2}-\frac{1}{2}\sum_{i=1}^{n+1}i\\
& = & \frac{\left(n+1\right)\left(n+2\right)\left(2n+5\right)}{12}-\frac{\left(n+1\right)\left(n+2\right)}{4}\\
& = & \frac{\left(n+1\right)\left(n+2\right)\left(n+3\right)}{6}
\end{eqnarray*} new rectangles.
So all in all we'd have this many rectangles:
\begin{eqnarray*}
\sum_{i=0}^{n-1}\frac{\left(i+1\right)\left(i+2\right)\left(i+3\right)}{6} & = & \frac{1}{6}\sum_{i=0}^{n-1}\left(i^{3}+6i^{2}+11i+6\right)\\
& = & \frac{1}{6}\left(\frac{n^{2}\left(n-1\right)^{2}}{4}\right)+\frac{\left(n-1\right)\left(n\right)\left(2n-1\right)}{6}+\frac{11}{6}\frac{n\left(n-1\right)}{2}\\
& & +n\\
& = & \boxed{\dfrac{1}{24}n\left(n+1\right)\left(n+2\right)\left(n+3\right)}
\end{eqnarray*}
SOLUTION
In the given case, we have $\frac{1}{24}\cdot8\cdot9\cdot10\cdot11=\boxed{660}$ rectangles all in all.
In the given case, we have $\frac{1}{24}\cdot8\cdot9\cdot10\cdot11=\boxed{660}$ rectangles all in all.
But this gives me an idea for a very powerful and not so ad-hoc technique.
Let's refine what it means to choose a rectangle by $(x_1,x_2,y_1,y_2)$. Essentially this is analogous to picking the coordinates of the upper right corner, then the coordinates of the lower left corner.
We can do just that to our staircase. For every point that can be an upper right corner, we count the number of lower left corners it can be paired with. Below is some clarification:
In the case of the staircase, it's just the multiplication table! In particular, here's the pattern for $n=8$:
\begin{eqnarray}
\sum_{i=1}^{n}\left(n+1-i\right)\sum_{j=1}^{i}j & = & \sum_{i=1}^{n}\frac{i\left(i+1\right)\left(n+1-i\right)}{2}\\
& = & \frac{1}{4}\sum_{i=1}^{n}i\left(i+1\right)\left(n+1-i\right)+\\
& & \left(n+1-i\right)\left(n+2-i\right)i\\
& = & \frac{n+3}{4}\sum_{i=1}^{n}i\left(n+1-i\right)\\
& = & \frac{n+3}{4}\left(\frac{n\left(n+1\right)^{2}}{2}-\frac{n\left(n+1\right)\left(2n+1\right)}{6}\right)\\
& = & \frac{1}{4}n\left(n+1\right)\left(n+3\right)\left(\frac{n+1}{2}-\frac{2n+1}{6}\right)\\
& = & \boxed{\frac{1}{24}n\left(n+1\right)\left(n+2\right)\left(n+3\right)}
\end{eqnarray} which gives us the same answer.
The second step in this computation (equation 2 above) may be a bit confusing. What I did was pair the $i$th term with the $(n+1-i)$th. In the case $n=8$, the first few steps will look like this:
\begin{eqnarray*}
\sum_{i=1}^{8}\left(9-i\right)\sum_{j=1}^{i}j & = & \sum_{i=1}^{8}\frac{i\left(i+1\right)\left(9-i\right)}{2}\\
& = & \frac{1\cdot2\cdot8}{2}+\frac{2\cdot3\cdot7}{2}+\frac{3\cdot4\cdot6}{2}+\frac{4\cdot5\cdot5}{2}\\
& & \frac{5\cdot6\cdot4}{2}+\frac{6\cdot7\cdot3}{2}+\frac{7\cdot8\cdot2}{2}+\frac{8\cdot9\cdot1}{2}\\
& = & \frac{1\cdot\left(2+9\right)\cdot8}{4}+\frac{2\cdot\left(3+8\right)\cdot7}{4}+\frac{3\cdot\left(4+7\right)\cdot6}{4}+\\
& & \frac{4\cdot\left(5+6\right)\cdot5}{4}+\cdots+\frac{8\cdot\left(9+2\right)\cdot1}{4}\\
& = & \frac{11}{4}\left(1\cdot8+2\cdot6+\cdots+8\cdot1\right)\\
& = & \frac{8+3}{4}\sum_{i=1}^{8}i\left(8+1-i\right)
\end{eqnarray*}








No comments:
Post a Comment